前言
这一篇博客的内容主要是最近通过课本以及在网络上找到的关于程序切片的学习资源的笔记。
程序切片的起源与发展
-
产生:1979年,美国Mark Weise首次在他的博士论文中提出了程序切片思想。
-
用途:程序切片技术在计算机学科的很多方面都产生了丰硕的结果;此外在软件开发的各个阶段、各种计算机语言的分析、形式化模型的分析以及软件测试方面都发挥了不可低估的作用。
-
原理:通过对源代码进行规划,可识别由于受到修改而影响的代码。
-
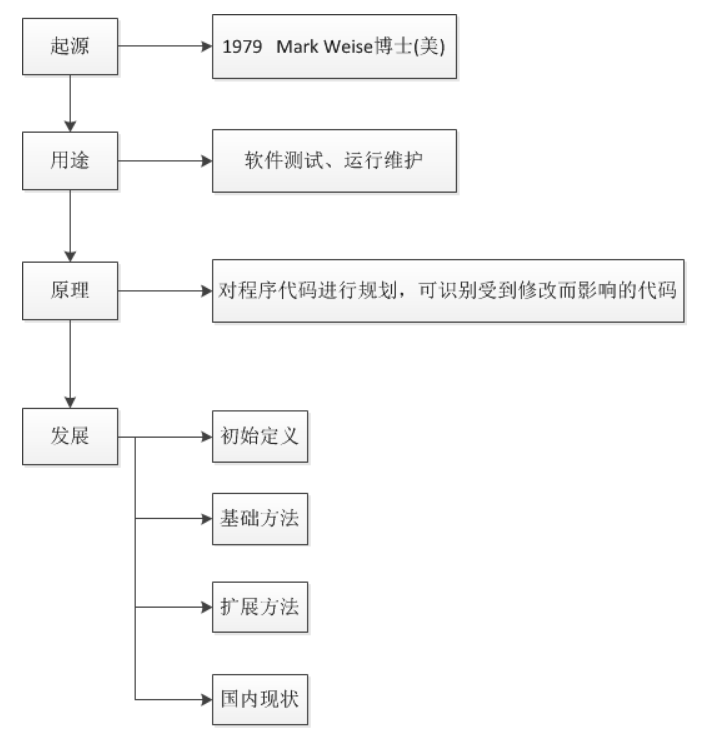
发展:程序切片的起源与发展将按照如下图所示顺序进行介绍。
-
初始定义:对程序P的切片准则C=(N,V)得到的切片S是从P中删去与N点处变量无关的指令和控制谓词所剩下的部分。切片S与源程序P对于切片准则C的语义是一致的。
-
基础方法:M.Weiser提出程序切片的基本概念以后,接下来是如何计算程序切片。于是M.Weiser在当时比较流行的程序控制流图(CFG)的基础上建立了数据流方程。通过求解数据流方程来获得相应的程序切片;称为数据流方程算法。1984年,K.J.Ottenstein 和 L.M.Ottenstein进一步改进(具体缘由后面给予说明),提出了程序依赖图(PDG),产生了基于PDG的图可达性算法;后来进一步改进,提出了系统依赖图(SDG),提出了基于SDG的两步遍历图可达性算法。基础算法的发展如下图所示。
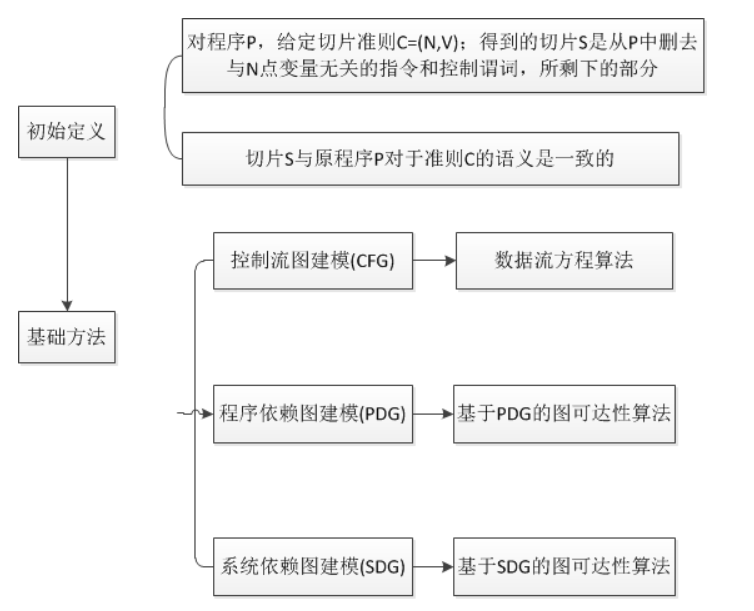
- 数据流方程算法的优缺点:
优点:产生了程序切片。
缺点:1、效率不高;此方法需要求解一系列的迭代方程,消耗的时间和空间多,且会导致误差累加。2、此方法只能解决基本结构的程序,对于含有过程的程序(特别是含有多个过程的程序)无法求解得到程序切片。
- 基于PDG的图可达性算法优缺点:
优点:此种方法的出现是计算程序切片方法的重大突破;不仅能够计算含有过程的程序切片,而且使程序切片的计算过程变的简单且可视化。
缺点:只能计算一个过程内的后向切片问题,不能计算含有多个过程的程序切片。
-
基于SDG的两步遍历图可达性算法: 解决了含多个过程程序的切片计算问题,基本趋于成熟。
-
扩展方法:在基于SDG的两步遍历图可达性算法出现之后,又产生了添加对象特征等的其他切片方案,大致顺序如下图所示。
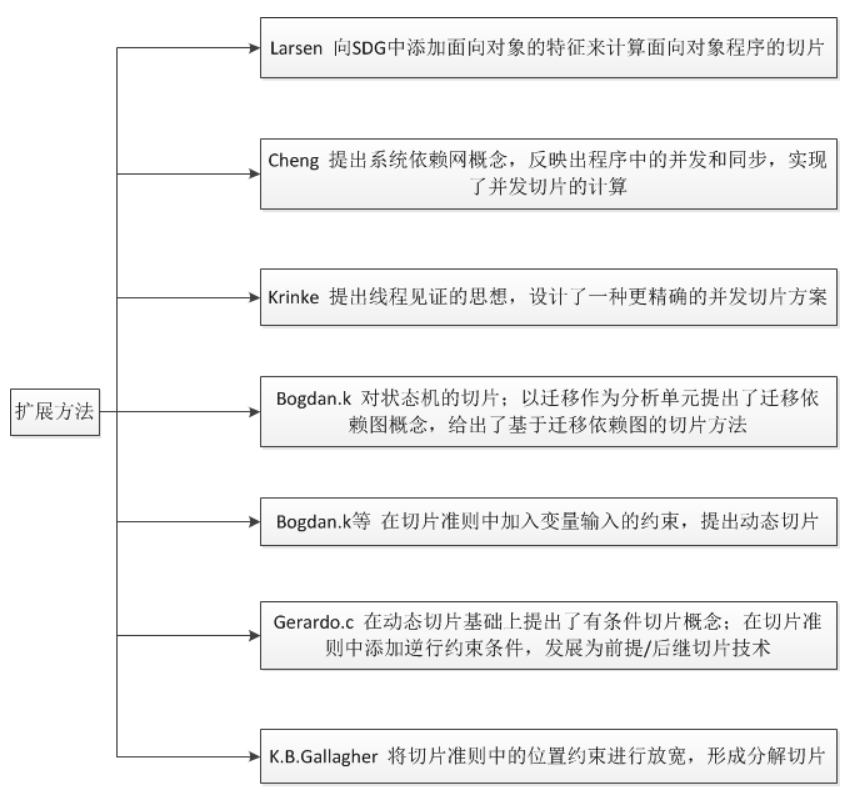
程序切片的类别
- 可执行与不可执行程序切片:最早由M.Weiser博士定义的程序切片是可执行的程序,他认为切片与源程序对某个特定的变量(包含在切片准则中的变量)而言,在程序的某个特定地方的语义是一致的。
一般而言,认为满足一下两个条件的程序切片称为M.Weiser程序切片:
一个程序切片对应一个特定的切片准则,记为<n,V>,其中V表示在n定义或使用变量的集合,n指程序中的某个点(一般指某条语句);
程序P的切片S可通过从P中删除零条或多条语句得到,但要保证程序P和切片S关于切片准则<n,V>的行为相同。
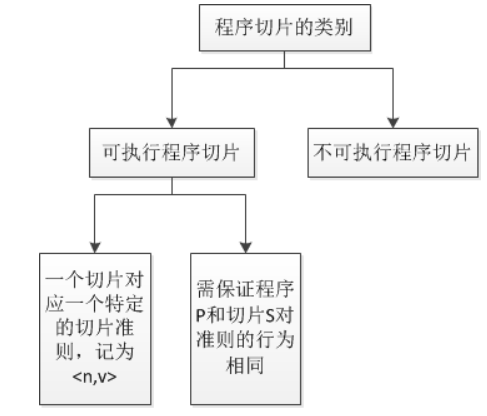
后来的研究者们对这一定义进行了推广,他们把一些不可执行的程序也包含进来,从而丰富了程序切片的内涵。定义程序切片的典型方法为:
给定某个程序P,程序切片准则<n,V>,程序P关于切片准则<n,V>的程序切片是由程序P中所有在n点对变量v属于V的值有影响的语句和控制谓词构成。显然,通过这种方式定义的程序切片不一定是可执行的。
- 静态切片、动态切片与有条件切片
根据程序切片的定义可知,切片准则是求程序切片的关键信息。对于切片准则<n,V>而言,n表示程序P中的某个兴趣点,V代表程序P中在n点定义或使用的变量。由不同的切片准则,可得到不同的切片。所以对切片准则进行研究,得到了静态切片、动态切片以及有条件切片。
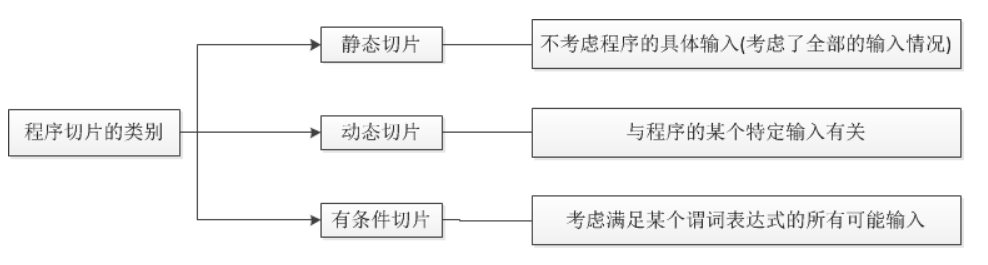
对于以上讨论的准则<n,V>,他没有考虑程序的具体输入是什么;即考虑的是所有可能的输入。若要考虑程序的某一个特定的输入Io情况下所有影响V在n点的值的语句和谓语组成的集合,称为动态切片,其准则是一个三元数组<n,V,Io>。
有条件切片是位于静态切片与动态切片之间的一种形式,是考虑满足某个谓词表达式的所有可能输入Ic,对应的切片准则为<n,V,Ic>。
静态切片、动态切片与有条件切片三者之间的关系为:静态切片包含动态切片;静态切片包含有条件切片。
- 后向切片与前向切片
根据切点(感兴趣点n)在切片S中的位置分为后向程序切片与前向程序切片。
后向切片是为了寻找与程序P中那些对某个兴趣点的变量有影响的语句和控制谓词,即应当在程序P中兴趣点的前面。
前向切片是为了寻找程序P中有哪些语句和谓词会受到n点的变量V的值的影响,即应当在程序P中兴趣点的后面。